The Theory

The full theory is described in the article. The overview presented below is based on the poster prepared for the Cosmic Controversies 2019 conference.

It is generally believed that Dark Matter can’t be baryonic gas (H, He) or dust because it would be opaque. This is in accordance with the classic Beer-Lambert law (and it derivatives) that relates gas transmittance to optical path length $l$ , concentration $c$ and molar absorptivity $\epsilon(\lambda)$ only, assuming molecules locality: $TR(\lambda)=10^{-lc\varepsilon(\lambda) }$
Increasing number of experiments show non-local matter properties, e.g. quantum entanglement, Bose-Einstein condensate, helium Young’s type double-slit experiment, etc

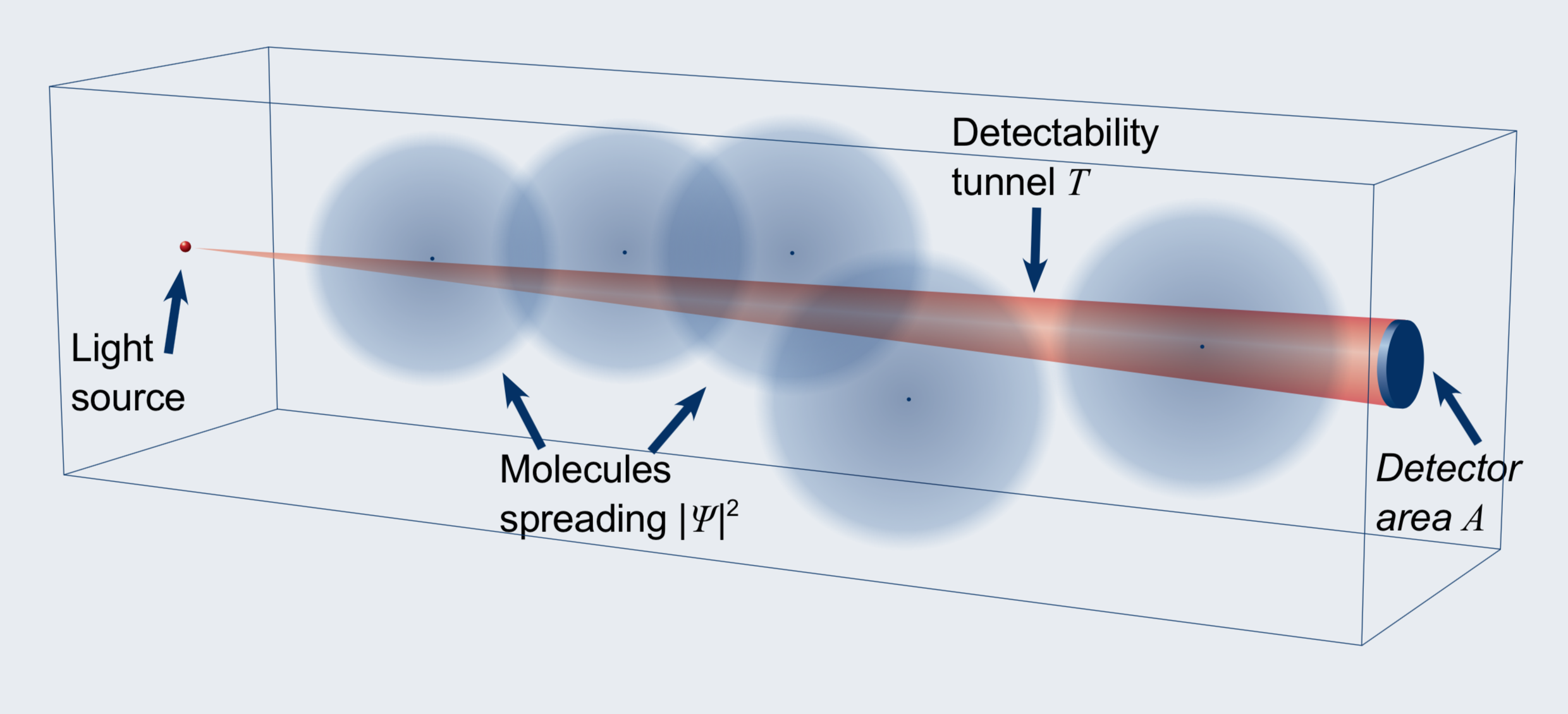
Model a non relativistic gas molecule as a gaussian wave packet
A molecule is free between consecutive collisions with either *photon or *molecule: mean free* time $\overline{t}$
Molecules’ wavefunctions spread according to the Schrödinger equation for a free particle, it is smeared gas
Assume a wavelenght dependend cross section $\sigma(\lambda)$ remains constant on spreading, i.e. constant Einstein coefficients
If a detector area $A$ is smaller than molecule spread, a photon scattering out of detectability tunnel $T$ can’t be observed, probability of possibly observed scattering event reads as: $P^{obs}\left ( \overline{t},\lambda \right )=C(\sigma(\lambda), \sigma_A, geometry)\int_T\left | \mathit{\Psi} (\boldsymbol{r}, \overline{t} ) \right |^2dr ,$ where $C$ depends on geometry of actual setup, total cross-section and detector dimensions and efficiency
Taking $N$ independent molecules, where incident photon may be scattered by any of them, a Markov chain is used for the transmittance equation: $TR ( \overline{t},\lambda )=\prod_{n=1}^N\left ( 1-P_n^{obs} ( \overline{t},\lambda ) \right )$
Analytical form of the transmittance lower limit may be presented

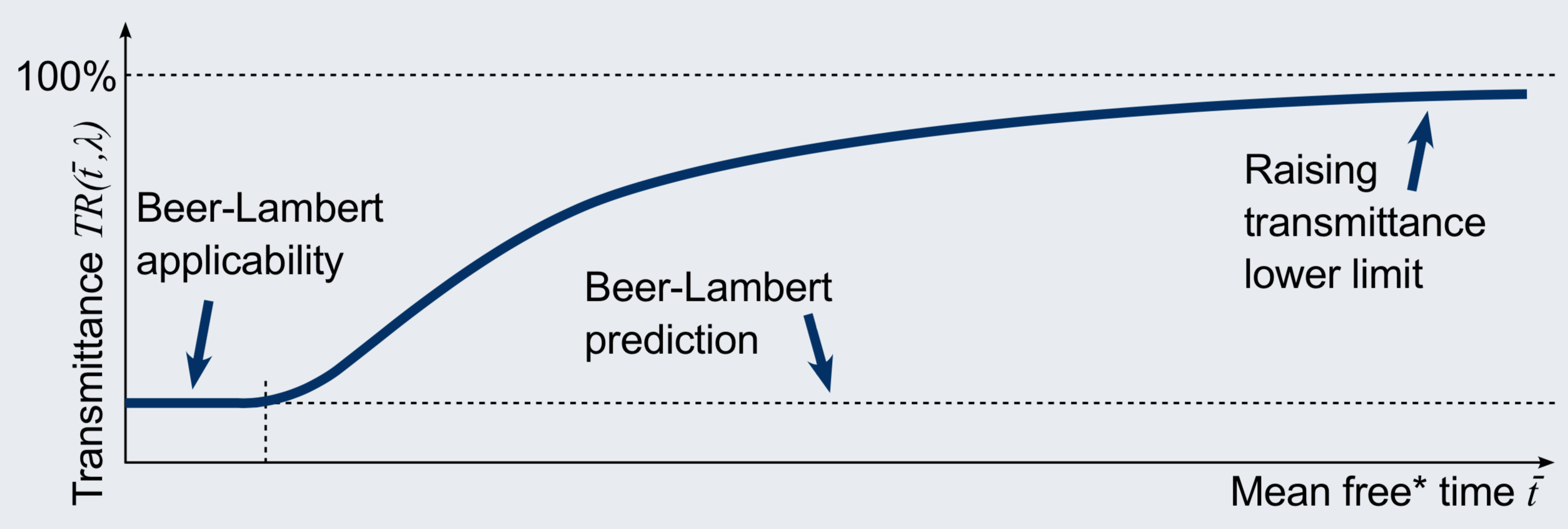
Transmittance of smeared gas depends also on a detector size and mean free* time $\overline{t}$
Raising mean free* time $\overline{t}$ leads to raising gas transmittance measured with a small detector:

$TR ( \overline{t},\lambda )\geqslant \prod_{n=1}^N\left [ 1- \frac{C(...)}{4} \left ( erf \left( \frac{dist_n-\sqrt{A}}{\sqrt2 stdev(\bar{t})} \right) \newline - erf \left( \frac{dist_n+\sqrt{A}}{\sqrt2 stdev(\bar{t})} \right) \right )^2 \right ]$

where $\Delta$ -initial position measurement accuracy, $m$ -molecule mass, $dist_n$ - distance from $\left \langle x_n \right \rangle$ to tunnel $T$ axis and $stdev(\bar{t})=\sqrt{\frac12 \left( \Delta^2+\frac{\hbar^2\bar{t}^2}{m^2\Delta^2} \right)}$
Transmittance smaller as detector gets bigger
Interstellar medium transmittance depends on background radiation intensity
Calculations confirm intragalactic radiation is so weak thay neutral atomic hydrogen (HI) may form smeared gas clouds
It is shown, the classic Beer-Lambert law is the first-order approximation of the proposed model

Achieved results interesting for QM measurement & decohorence discussions
A variety of possible laboratory or orbital experiments for detecting smeared gas are proposed in the paper
Geocorona may be smeared (H) gas as its observed „density” depends on Earth shadow & Sun activity
Baryonic (H, He) Dark Matter would be ultra diluted gas, intragalactic radiation is weak enough so clouds of smeared gas may be a component of Dark matter